ab是圆o的直径 如图，AB为⊙O的直径，AC为⊙O的弦，AD平分...

　　导读：本文所考察的知识点是ab是圆o的直径,详细到1、圆与直线相切；2、三角形全等；3、相似的知识三个小知识点，因此解答本题的关键是需要考生“会判断圆与直线相切及三角形全等及相似的知识”。

        试题描述       

如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E.

　　

 

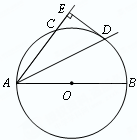
　　(1)判断直线DE与⊙O的位置关系，并说明理由;

　　(2)若AE=8，⊙O的半径为5，求DE的长.

        试题答案       

　　答案

　　(1)直线DE与⊙O相切;(2)4

　　解析试题分析：1)直线DE与⊙O相切.

　　理由如下：

　　连接OD.

　　∵AD平分∠BAC，

　　∴∠EAD=∠OAD.

　　∵OA=OD，

　　∴∠ODA=∠OAD.

　　∴∠ODA=EAD.

　　∴EA∥OD.

　　∵DE⊥EA，

　　∴DE⊥OD.

　　又∵点D在⊙O上，∴直线DE与⊙O相切.

　　(2)

　　方法一：

　　

 

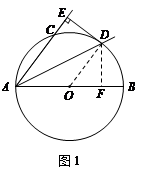
　　如图1，作DF⊥AB，垂足为F.

　　∴∠DFA=∠DEA=90°.

　　∵∠EAD=∠FAD，AD=AD，

　　∴△EAD≌△FAD.

　　∴AF=AE=8，DF=DE.

　　∵OA=OD=5，∴OF=3.

　　在Rt△DOF中，DF==4.

 

　　∴DE=DF=4.

　　方法二：

　　如图2，连接DB.

　　

 

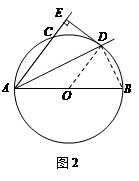
　　∵AB为⊙O的直径，

　　∴∠ADB=90°.

　　∴∠ADB=∠AED.

　　∵∠EAD=∠DAB，

　　∴△EAD∽△DAB.

　　∴

.

 

　　即.解得.

 

　　在Rt△ADE中，=4.

 

　　方法三：

　　如图3，作OF⊥AD，垂足为F.

　　

 

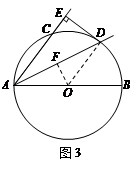
　　∴AF=AD，∠AFO=∠AED.

 

　　∵∠EAD=∠FAO，

　　∴△EAD∽△FAO.

　　∴

 

　　即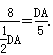.解得

.

 

　　在Rt△ADE中，DE==4

 

　　考点：圆

　　名师点评：本题所考查的知识点涉及到了圆的相关知识，如AB为⊙O的直径（ab为圆O的直径），AC为⊙O的弦。与直线相切，三角形全等和三角形相似，首先分析圆与直线相切，再根据三角形全等及相似的知识点作相关的辅助线，如方法3中的——作OF⊥AD，垂足为F.进一步的演算解得解得，然后计算出DE=4的演算。

　　本题难度：中等难度。

本文来源于52ij试题网http://shiti.52ij.com/，52ij试题网有小学试题、初中试题及高中试题，初中试卷和高中试卷等，欢迎大家继续阅读学习。如有什么问题或建议请加52ij试题网的QQ群6538112沟通交流。