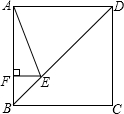
正方形ABCD的边长为4 如图所示点E在对角线BD上且角BAE=22.5度...

本题是大家所熟悉的正方形ABCD的边长为4，然后相应的与三角形挂钩，最后需要计算出三角形的某一边边长的问题，所涉及到知识点主要是三角形的相关知识。

题目：如图，正方形ABCD的边长为4，点E在对角线BD上，且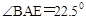，EF⊥AB，垂足为F，则EF的长为

A．1

B．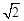

C．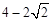

D．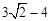

答案：C

解析：分析：在正方形ABCD中，∠ABD=∠ADB=45°，
∵∠BAE=22.5°，∴∠DAE=90°－∠BAE=90°－22.5°=67.5°。
在△ADE中，∠AED=180°-45°-67.5°=67.5°，∴∠DAE=∠ADE。∴AD=DE=4。
∵正方形的边长为4，∴BD=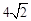。∴BE=BD－DE=。
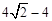∵EF⊥AB，∠ABD=45°，∴△BEF是等腰直角三角形。
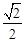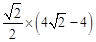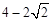∴EF=BE==。故选C。

点评：本题所考查的知识点是三角形，属于正方形ABCD的边长为4，然后给出三角形的条件最后计算三角形边长一类的选择题，主要是抓住已知条件正方形的边长为4就可以推算出BD和BE的边长，又因为EF垂直AB且角ABD是45度，即可判断出三角形是等腰直角三角形，进一步演算出答案。

难度：易

本文来源于52ij试题网http://shiti.52ij.com/，52ij试题网有小学试题、初中试题及高中试题，初中试卷和高中试卷等，欢迎大家继续阅读学习。如有什么问题或建议请加52ij试题网的QQ群6538112沟通交流。